JEE 2016 :: Advanced 2016 :: Mathematics 2016

• Advanced 2016 - Physics 2016
• Advanced 2016 - Chemistry 2016
• Advanced 2016 - Mathematics 2016

Let  $\hat{u}=u_{1}\hat{i}+u_{2}\hat{j}+u_{3}\hat{k}$ be a unit vector  R³ and $\hat{w}=\frac{1}{\sqrt{6}}({}\hat{i}+\hat{j}+2\hat{k})$. Given that there exists vector  $\overrightarrow{v}$  in  $R^{3}$ , such  that  $|\hat{u}+\vec{v}|=1$ and  $\hat{w}.(\hat{u}+\vec{v})=1$   which of the following statement(s) is/are correct?

Answer:

Explanation:

Let θ be the angle between  $\hat{u} $ and $\vec{v} $

$\therefore|\hat{u} \times \overrightarrow{v}|=1\Rightarrow|\hat{u}|\overrightarrow{v}|\sin \theta=1$

$\therefore |\overrightarrow{v}| \sin \theta=1 $ $[\therefore |\hat{u}|=1]$  .......(i)

Clearly, there may be infinite vectors

 $\overrightarrow{OP}=\overrightarrow{v}$ , such that  P is always 1 unit distance from  $\hat{u}$.

$\therefore$    Option (b) is correct.

Again, let Φ be the angle between $\hat{w}$ and  $\hat{u}\times\overrightarrow{v}.$

$\therefore \hat{w}.(\hat{u}\times\overrightarrow{v})=1\Rightarrow |\hat{w}||\hat{u}\times\overrightarrow{v}|\cos \phi =1$

$\Rightarrow \cos \phi=1\Rightarrow\phi=0$

Thus,    $\hat{w}=\hat{u}\times \overrightarrow{v}$

Now, if  $\hat{u}$ lies in XY-plane, then

$\begin{vmatrix}\hat{i} & \hat{j}& \hat{k} \\u_{1} & u_{2}&0 \\ v_{1}&v_{2}&v_{3} \end{vmatrix}$

 or      $\hat{u}=u\hat{i}+u_{2}\hat{j}$

     $\therefore\hat{w}=(u_{2}v_{3})\hat{i}-(u_{1}v_{3})\hat{j}+(u_{1}v_{2}-v_{1}u_{2})\hat{k}$

 $\therefore\hat{w}=\frac{1}{\sqrt{6}}(\hat{i}+\hat{j}+2\hat{k})$

$\therefore$     $u_{2}v_{3}=\frac{1}{\sqrt{6}}\Rightarrow u_{1}v_{3}=\frac{-1}{\sqrt{6}}$

$\Rightarrow  \frac{u_{2}v_{3}}{u_{1}v_{3}}=-1$ or   $|u_{1}|=|u_{2}|$

$\therefore$ Option (c) is correct.

Now, if  $\hat{u}$ lies un XZ-plane, then  $\hat{u}= u_{1}\hat{i}+u_{3}\hat{k}$

    $\therefore$       

$\begin{vmatrix}\hat{i} & \hat{j}& \hat{k} \\u_{1} & 0&u_{3} \\ v_{1}&v_{2}&v_{3} \end{vmatrix}$

$\Rightarrow w=(-v_{2}u_{3})\hat{i}-(u_{1}v_{3}-u_{3}v_{1})\hat{j}+(u_{1}v_{2})\hat{k}$

$\Rightarrow \hat{w}=\frac{1}{\sqrt{6}}(\hat{i}+\hat{j}+2\hat{k})$

$= -v_{2}u_{3}=\frac{1}{\sqrt{6}}$  and  $u_{1}v_{2}=\frac{2}{\sqrt{6}}$

$=|u_{2}|=2|u_{3}|$

  $\therefore$  Option (d) is incorrect

Let f:R→ (0,∞) and g: R→ R be twice differentiable functions such that f ’’ and g’’ are continuous functions on R

 Suppose  $f'(2)=g(2)=0, f''(2)\neq 0$ and $g'(2)\neq 0$, If  $\lim_{x \rightarrow 2}\frac{f(x)g(x)}{f'(x)g'(x)}=1$,  then

Answer:

Explanation:

Here,  $\lim_{x \rightarrow 2}\frac{f(x).g(x)}{f'(x).g'(x)}=1$

 $\Rightarrow \lim_{x \rightarrow 2}\frac{f(x)g'(x)+f'(x)g(x)}{f''(x)g'(x)+f'(x)g''(x)}=1$

  [using L' hospital's rule]

$\Rightarrow   \frac{f(2)g'(2)+f'(2)g(2)}{f''(2)g'(2)+f'(2)g''(2)}=1$

$\Rightarrow       \frac{f(2)g'(2)}{f''(2)g'(2)}=1$

 $[\therefore f'(2)=g(2)=0]$

  $\Rightarrow f(2)=f''(2)$           ...............(i)

$\therefore$            $f(x)-f"(x)=0$ , for atleast one x ε R

 $\Rightarrow$ Option (d) is correct

   Also, f:R → (0,∞ )

$\Rightarrow$       f(2)>0

$\therefore$   f''(2)=f(2)>0  [ from Eq .(i)]

Since f '(2)=0 and f''(2) >0

$\therefore$ f(x) attains local minimum at x=2

$\Rightarrow$  Option (a) is correct.

Let f(x)$=\lim_{n \rightarrow \infty}\left[\frac{n^{n}(x+n)(x+\frac{n}{2})....(x+\frac{n}{n})}{n!(x^{2}+n^{2})(x^{2}+\frac{n^{2}}{4}).....(x^{2}+\frac{n^{2}}{n^{2}})}\right]^{\frac{x}{n}}$

for all x=0, then

Answer:

Explanation:

Here, f(x)

  $=\lim_{n \rightarrow \infty}\left[\frac{n^{n}(x+n)(x+\frac{n}{2})....(x+\frac{n}{n})}{n!(x^{2}+n^{2})(x^{2}+\frac{n^{2}}{4}).....(x^{2}+\frac{n^{2}}{n^{2}})}\right]^{\frac{x}{n}}$

     x>0

Taking  log on both sides, we get  $\log_{e}[f(x)]$

             $  =\lim_{n \rightarrow \infty}\log\left[\frac{n^{n}(x+n)(x+\frac{n}{2})....(x+\frac{n}{n})}{n!(x^{2}+n^{2})(x^{2}+\frac{n^{2}}{4}).....(x^{2}+\frac{n^{2}}{n^{2}})}\right]^{\frac{x}{n}}$

$=\lim_{n \rightarrow \infty}\frac{x}{n}.\log \left[\frac{\prod_{r=1}^{n}(x+\frac{1}{r/n})}{\prod_{r=1}^n(x^{2}+\frac{1}{(r/n)^{2}})\prod_{r=1}^{n}(r/n)}\right]$

$=x\lim_{n \rightarrow \infty}\frac{1}{n}\sum_{r=1}^{n}\log\left[\frac{x+\frac{n}{r}}{(x^{2}+\frac{n^{2}}{r^{2}})(r/n)}\right]$

$=x\lim_{n \rightarrow \infty}\frac{1}{n}\sum_1^n \log \left[\frac{\frac{r}{n}.x+1}{\frac{r^{2}}{n^{2}}.x^{2}+1}\right]$

Converting summation into definite integration, we get  $\log_{e}[f(x)]$

$=x\int_{0}^{1} \log (\frac{xt+1}{x^{2}t^{2}+1})dt$

put $tx=z\Rightarrow xdt=dz$

$\therefore  \log_{e}[f(x)]=x\int_{0}^{x} \log(\frac{1+z}{1+z^{2}})\frac{dz}{x}$

$\Rightarrow  \log_{e}[f(x)]=\int_{0}^{x} \log(\frac{1+z}{1+z^{2}})dz$

Using Newton-Leibnitz formula, we get

$\frac{1}{f(x)}.f'(x)=\log(\frac{1+x}{1+x^{2}})......(i)$

Here x=1,

   $\frac{f'(1)}{f(1)}=\log(1)=0$

$\therefore$          F'(1)=0

Now,sign scheme of f'(x) is shown below

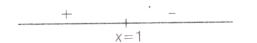
               $\therefore$  At x=1, function attains maximum

 Since, f(x) increases on (0,1)

                         f(1)>f(1/2)

$\therefore$   Option (a) is incorrect

                               f(1/3)<f(2/3)

$\therefore$    Option (b) is correct

 Also ,f'(x)<0, when x>1

          $\Rightarrow$   f'(2)<0

$\therefore$ Option(c) is correct

         Also,  $\frac{f'(x)}{f(x)}=\log( \frac{1+x}{1+x^{2}})$

$\therefore$   $\frac{f'(3)}{f(3)}-\frac{f'(2)}{f(2)}=\log(\frac{4}{10})-\log(\frac{3}{5})$

                              =  $\log(2/3)<0$

$\Rightarrow  \frac{f'(3)}{f(3)}<\frac{f'(2)}{f(2)}$

    $\therefore$  Option (d) is incorrect

Let $a,b\epsilon R$ and f:R→ R  be defined by  $f(x)=a\cos(|x^{3}-x|)+b|x|\sin(|x^{3}+x|)$. Then f is 

Answer:

Explanation:

$f(x)=a\cos(|x^{3}-x|)+b|x|\sin(|x^{3}+x|)$

   if  $x^{3}-x\geq0$

$\Rightarrow  \cos|x^{3}-x|=\cos(x^{3}-x)$

            $x^{3}-x\leq0$

$\Rightarrow  \cos|x^{3}-x|=\cos(x^{3}-x)$

$\therefore  \cos(|x^{3}-x|)=\cos(x^{3}-x), \forall x\epsilon R$   .........(i)

Again , if   $x^{3}+x\geq0$

    $\Rightarrow  |x|\sin(|x^{3}+x|)=x\sin(x^{3}+x)$

$x^{3}+x\leq 0$

 $\Rightarrow  |x|\sin(|x^{3}+x|)=-x\sin(-(x^{3}+x)) $

$\therefore $                 $|x|\sin(|x^{3}+x|)=x\sin(x^{3}+x), \forall x\epsilon R$  .......(ii)

$\Rightarrow f(x)=a\cos(|x^{3}-x|)+b|x|\sin(|x^{3}+x|)$

$\therefore $  $f(x)= a\cos (x^{3}-x)+bx \sin (x^{3}+x)$     ........(iii)

which is clearly sum and composition of differential functions.

    Hence, f(x) is always continuous  and differentiable

Let P be the image of the point (3,1,7) with respect to the plane  x-y+z=3 Then, the equation of the plane passing through P and containing the straight line  $\frac{x}{1}=\frac{y}{2}=\frac{z}{1}$ is

Answer:

Explanation:

Let image of Q(3,1,7) w.r.t

         x-y+z=3 be $P (\alpha,\beta,\gamma)$

               $\therefore  \frac{\alpha-3}{1}=\frac{\beta-1}{-1}=\frac{\gamma-7}{1}$

           $=\frac{-2(3-1+7-3)}{1^{2}+(-1)^{2}+(1)^{2}}$

            $\Rightarrow\alpha-3=1-\beta=\gamma-7=-4$

$\therefore$     $\alpha=-1,\beta=5,\gamma=3$

Hence, the image of Q(3,1,7) is P(-1,5,3) .

        to find equation of plane passing through P(-1,5,3) and containing  $\frac{x}{1}=\frac{y}{2}=\frac{z}{1}$

$\Rightarrow$ $\begin{bmatrix}x-1 & y-0 & z-1 \\1-0 & 2-0 &1-0\\-1-0&5-0&3-0 \end{bmatrix}=0$

$\Rightarrow x (6-5)-y(3+1)+z(5+2)=0$

$\therefore$    x-4y+7z=0

• Advanced 2016 - Physics 2016
• Advanced 2016 - Chemistry 2016
• Advanced 2016 - Mathematics 2016